Prototyping an adaptive mesh refinement library in JAX

2025-05-18

I was lucky enough to spend the last six weeks or so on paternity leave from my job at Pasteur Labs, where I'm prototyping various differentiable physics workflows in JAX. During baby downtimes, I traded perhaps more sleep hours than I should have to hash out a quick prototype of an adaptive mesh refinement library built on JAX.

Obviously I had to name it Jack's AMR .

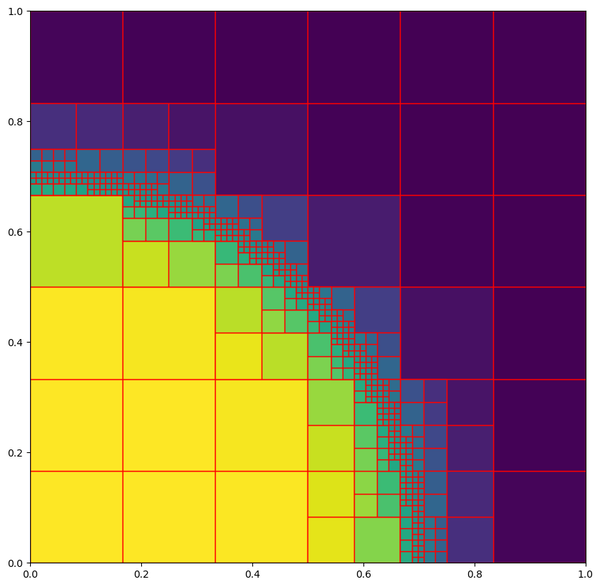
JAX presents an interesting challenge for designing an adaptive mesh refinement (AMR) library. The core idea of AMR is that the mesh dynamically resizes itself to represent your PDE solution with the best tradeoff of accuracy and efficiency. The programming model of JAX, however, absolutely discourages dynamic allocations. When jax.jit traces and compiles your code, it fixes a known shape for every array that appears in the program. Arrays can't be resized without recompiling the jitted block.

Without the ability to dynamically allocate grids, we lose a lot of flexibility. Our AMR system will always be operating with the peak amount of resident memory: all of the memory we might ever need to use must be allocated up front. However, not all of the performance benefits of AMR come from dynamically allocating grid cells. Much (most?) of the benefit comes from saving work on non-existent cells. There is a JAX-friendly approach that hopefully preserves most of this advantage: allocate space for all the cells in our "budget", but only activate them when they are necessary. The total budget of cells at the finest resolution can be much less than the size of the grid if it were refined everywhere to that resolution. Moreover, inactive cells can be skipped when performing flux calculations, saving more FLOPs compared to the globally refined baseline.

The current implementation includes:

• Datastructures to represent an AMR grid and scalar functions defined on it.
• A refine_to_approximate function to refine the grid for approximating a supplied analytic expression. This was used to create the above example image.
• A refine_and_coarsen function to modify a grid and grid function by refining and coarsening cells based on the percentile values of a refinement indicator.
• A flux_divergence function to calculate \(\nabla \cdot F(q)\) for a flux function \(F\) and grid function \(q\).

The latter requires a particularly interesting implementation in JAX. Because we can't construct dynamically-sized arrays, it is impossible to go around and collect all the cells neighboring a particular reference cell. Instead, we begin at the finest level of refinement, and compute fluxes across each face at that level. We then observe that a \(2n+1 \times 2n\) block of faces at level \(k+1\) can be coarsened to a block of \(n+1 \times n\) faces at level \( k \) via a simple aggregation. In blocks where level \(k+1\) is active, these aggregated face fluxes serve as the source of truth for fluxes at level \( k \). Further aggregation gives us a canonical array of fluxes at levels \( k-1 \), \( k-2 \), and so on for each level. The final flux divergence calculation is a simple differencing operation on arrays of fluxes at each level, some of which are computed between cells at that level and some of which have been aggregated from finer levels.

The process of implementing this library was highly instructive for my understanding of JAX. Now that I have a working prototype of this basic functionality, there are some clear opportunities for enhancements:

• Higher-order cell representations, particularly for high-order discontinuous Galerkin methods.
• Multiple-component grid functions
• Mesh smoothing: don't allow neighboring cells to differ by more than one level.
• More sophisticated refinement criteria. This is much easier with higher-order cells, since you have local gradient information.
• More accurate prolongation and restriction operators. Prolonging a piecewise constant solution by copying values gives very poor-looking results indeed.